学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとうございます。 開設以来、多くの皆様にご利用いただいております本ブログは、 より皆様のお役に立てるよう、2020年10月30日より形を変えてリニューアルします。 以下、弊社本部サイト『受験対策情報』にて記事を掲載していくこととなりました。 『受験対策情報』https://www.sakusakura.jp/examination/ 『受験対策情報』では、中学受験/高校受験/大学受験に役立つ情報、 その他、勉強に役立つ豆知識を掲載してまいります。 ぜひご閲覧くださいませ。今後とも宜しくお願い申し上げます。 |
こんにちは、サクラサクセスです。
このブログでは、サクラサクセスの本物の先生が授業を行います!
登場する先生に勉強の相談をすることも出来ます!
"ブログだけでは物足りない"と感じたあなた!!
ぜひ無料体験・相談をして実際に先生に教えてもらいませんか?
さて、そろそろさくらっこ君と先生の授業が始まるようです♪
今日も元気にスタート~!
大月先生
今日だけ数学担当の大月です。
さくらっこくん、よろしくね。

今日はどんなことをするのかな?
大月先生
今日は、2次方程式の見分け方を解説しますね。
早速だけど、
さくらっこくんは2次方程式がどんなものか、説明できるかな?

1次方程式とは違って、Xが2乗されてるものだよね!
大月先生
さくらっこくん、着眼点はいいよ!
ただ、少し惜しいね。
2次方程式っていうのは、一般的に
ax2+bx+c=0(ただし、a≠0)
大月先生
で、表されます。
それじゃ、たとえを出してみますね。
ここに、2つ式があります。
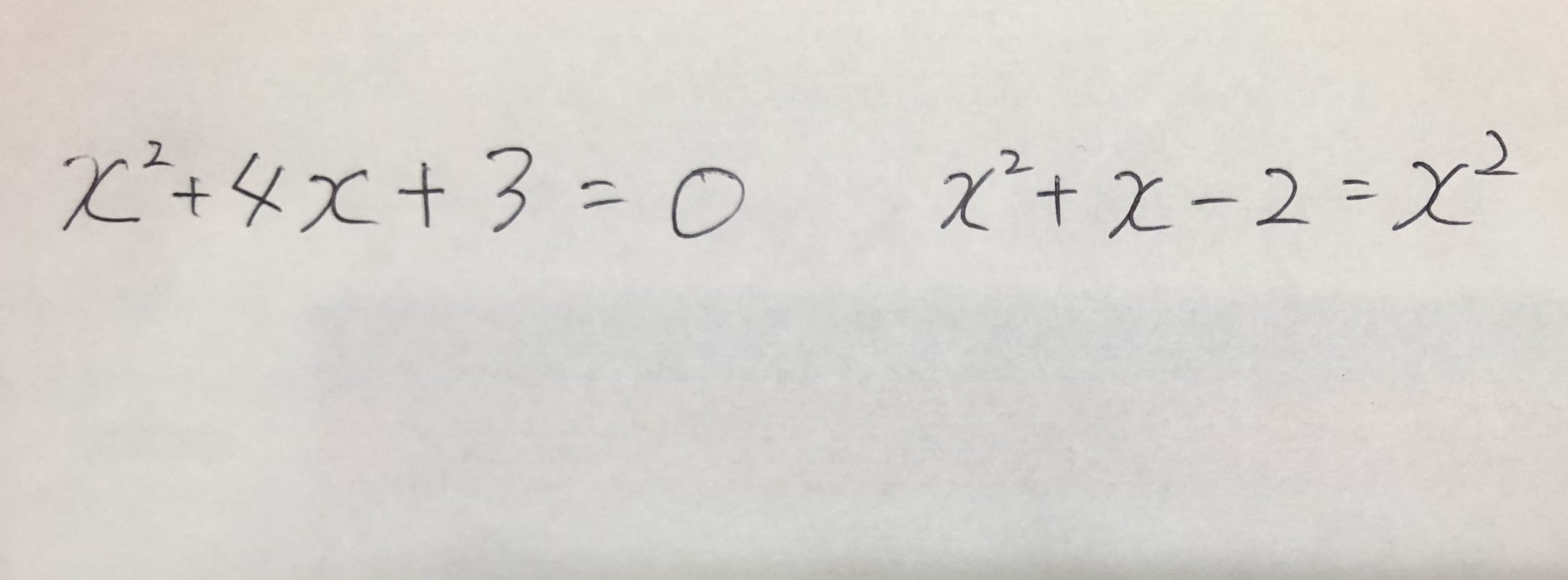
この二つのどちらかは、2次関数ではないんです。

どうやって見分けているのかな?
大月先生
この二つを、それぞれまとめてみましょう。

x2が式に入っていたとしても、まとめてみると1次関数になってしまいますよね。
なので一概に、『x2』が式にあるからといって、2次関数とおもってはダメなんです。
つまり2次関数は、
移行して整理すると『(xの2次式)=0』の形に変形できる方程式
ということです。
上記で上げた式は、わかりやすい式としての例ですが、
テストや試験になると、もっと複雑な式で出てくることもあります…!
まずは落ち着いて式を移行して整理してみると、
問題解決できるかもしれないですね(^^)
もし複雑な式が出てきたら、ぜひ試してみてください。

式を一旦整理して、その上で判断して対応していかなきゃいけないんだね。
複雑な式のまま考えるんじゃなくて、しっかりまとめてから考えるようにしてみる!
大月先生ありがとうございました!!
最後までお読みくださりありがとうございます♪
実際に、このブログに登場した先生に勉強の相談をすることも出来ます!
「ブログだけでは物足りない」、「もっと先生に色々教えてほしい!」と感じたあなた、
ぜひ無料体験・相談をして実際に先生に教えてもらいましょう!
友だちも誘って、ぜひ一度体験しに来てくださいね!

