学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとうございます。 開設以来、多くの皆様にご利用いただいております本ブログは、 より皆様のお役に立てるよう、2020年10月30日より形を変えてリニューアルします。 以下、弊社本部サイト『受験対策情報』にて記事を掲載していくこととなりました。 『受験対策情報』https://www.sakusakura.jp/examination/ 『受験対策情報』では、中学受験/高校受験/大学受験に役立つ情報、 その他、勉強に役立つ豆知識を掲載してまいります。 ぜひご閲覧くださいませ。今後とも宜しくお願い申し上げます。 |
こんにちは、サクラサクセスです。
このブログでは、サクラサクセスの本物の先生が授業を行います!
登場する先生に勉強の相談をすることも出来ます!
"ブログだけでは物足りない"と感じたあなた!!
ぜひ無料体験・相談をして実際に先生に教えてもらいませんか?
さて、そろそろさくらっこ君と先生の授業が始まるようです♪
今日も元気にスタート~!
藤田先生
数学担当の藤田です。
中学生は気付けば中間まで約1か月…
高校生はもう中間テストが始まっているところもあるかもしれません。
しっかり中間テストに向けて対策しておきましょう!
不安であれば対策会も活用しましょう!

中間テストに向けて、しっかり準備をしておかなきゃね!!
藤田先生
さて、本題に入っていきましょう!
今回のテーマは前回に引き続き「割合」です!
前回は割合を求めました。
ここで補足しておきます。
「は」にあたる部分は「くらべる量」で、基準になるものと比較される数量になります。
「の」にあたる部分は「もとになる量」で、基準になる数量です。
今回はこの「くらべる量」の求め方についてです。
『くらべる量』の求め方
藤田先生
まずは問題。
1800円の4割は何円でしょう。
さくらっこくん、分かるかな??

藤田先生
ではこの問題はどうだろう?
1800円の0.4倍は何円でしょう。
これだと分かりやすいかな?

計算すると、720円だね!
藤田先生
そう、答えは720円だね!
もちろん、1800×0.4=720で求められるね!
前回、割合を求めるときにこんなことを言ったのを覚えているかな?
割合を求めるために計算して、それによって出た答えは「倍」で、
10倍したら「割」、100倍したら「%」になったよね!
ということは逆に考えると…
「割」を10で割ると「倍」になるし、
「%」を100で割ると、これも「倍」という表現になります。
先ほどの問題を見てみましょう。
「1800円の4割」の「4割」は4を10で割って「0.4倍」ということになります。
「○○倍」と言われたらかけ算をするのはなんとなくわかりますね!
「○○の△△割」または「○○の△△%」と言われたら、
10や100で割って「倍」という表現に直すと考えやすくなるからね!
これが理解できた人は次の問題にチャレンジ!
練習問題
640人の65%は何人でしょう?
※答えは一番最後にあるよ!
さて、今回は「くらべる量」の求め方について説明しました。
残りは「もとになる量」だけですが…
さくらっこくんは「みはじ」とか「きはじ」とか知ってるかな?

藤田先生
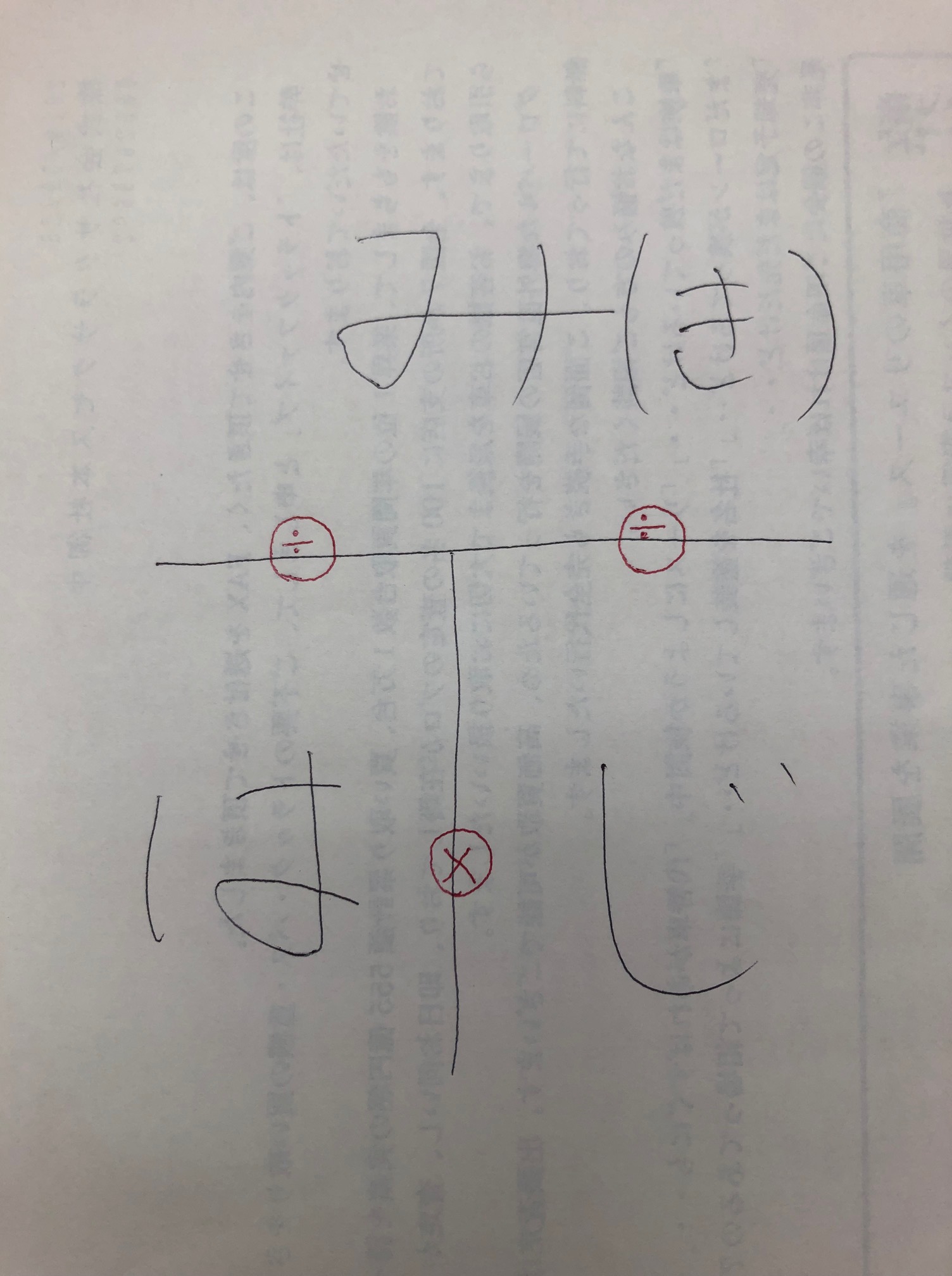
そう、道のり(距離)、速さ、時間の関係が分かるために図でかくよね!
上に「み(き)」を書いて下に「は」と「じ」があるよね!
実は割合も似たものがあって「くもわ」で覚えるんだ!
上に「く」を書いて下に「も」と「わ」を書くんだけど…
「く」は「くらべる量」、「も」は「もとになる量」、「わ」は「割合」のことだよ!
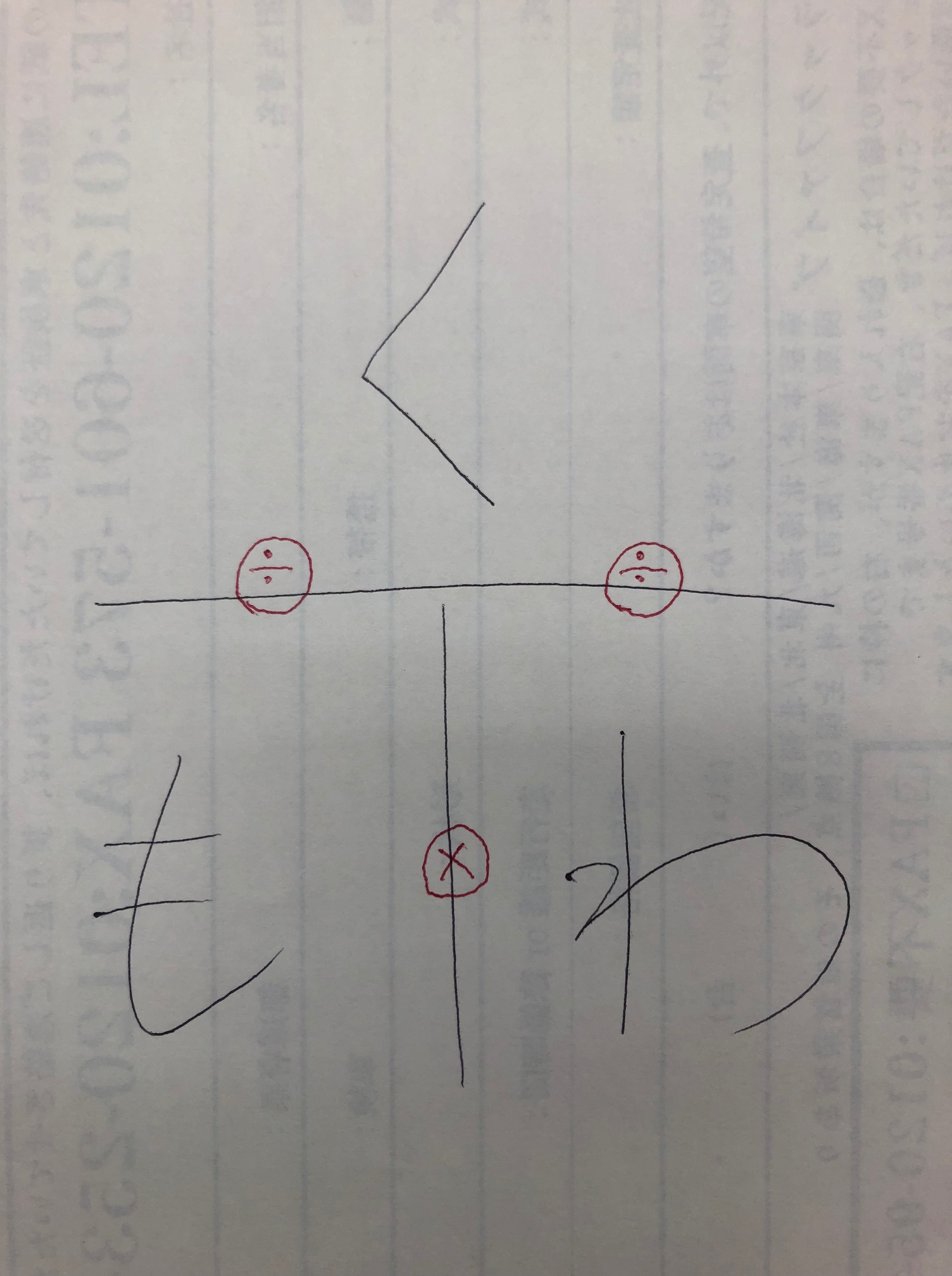
く=も×わ
も=く÷わ
わ=く÷も
だね!
これが難しかったら「はの倍」で覚えてもいいよ!
「○○は□□の△△倍」に対応します!
上に「は」を書いて下に「の」と「倍」を書くからね!
さっきも言ったことだけど、「割」や「%」は「倍」と同じだからね!
は=の×倍
の=は÷倍
倍=は÷の
前回のまとめで出てきた「は」÷「の」があるね!
「くもわ」や「はの倍」をしっかり覚えておいて、
あとは問題文からどの数字を使っていいかをしっかり読み取ることができたら、
かけ算かわり算か迷うことはなくなるね!
使いこなせるようになるためには、何回も問題を解くこと!
これを読んで理解できた!………で、終わりにしないようにね!
今回はここまで!
割合が少しでもできるようになってくれたり、
割合のイメージが少しでも良くなればと思っています!
次回も頑張りましょう!!

使いこなすためには、色々な問題を解いていかなきゃね!
今日の内容を活かして、計算問題に挑戦するぞ~!!
藤田先生ありがとうございました!!
藤田先生
練習問題の答えは416人です!
65%を100で割って0.65倍という表現に直すと、
640×0.65で求めることができますね!
最後までお読みくださりありがとうございます♪
実際に、このブログに登場した先生に勉強の相談をすることも出来ます!
「ブログだけでは物足りない」、「もっと先生に色々教えてほしい!」と感じたあなた、
ぜひ無料体験・相談をして実際に先生に教えてもらいましょう!
友だちも誘って、ぜひ一度体験しに来てくださいね!

