中学3年生向け！平方根はこうやって解く！平方根を基本から徹底解説！③

学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ

学習内容解説ブログをご利用下さりありがとうございます。

開設以来、多くの皆様にご利用いただいております本ブログは、
より皆様のお役に立てるよう、2020年10月30日より形を変えてリニューアルします。

以下、弊社本部サイト『受験対策情報』にて記事を掲載していくこととなりました。

『受験対策情報』https://www.sakusakura.jp/examination/

『受験対策情報』では、中学受験/高校受験/大学受験に役立つ情報、
その他、勉強に役立つ豆知識を掲載してまいります。

ぜひご閲覧くださいませ。今後とも宜しくお願い申し上げます。

こんにちは、サクラサクセスです。
このブログでは、サクラサクセスの本物の先生が授業を行います！
登場する先生に勉強の相談をすることも出来ます！
"ブログだけでは物足りない"と感じたあなた!!
ぜひ無料体験・相談をして実際に先生に教えてもらいませんか？
さて、そろそろさくらっこ君と先生の授業が始まるようです♪
今日も元気にスタート～！
　
　
　
みなさんこんにちは！

夏休みもそろそろ折り返し地点ですね！

今日は平方根の解説の続きをします！

前回の√についての説明で、なぜ√を使うかご理解いただけましたか？

忘れちゃったよ！という方はコチラからご確認ください。

>>前回のブログはコチラから【中学3年生向け！平方根はこうやって解く！平方根を基本から徹底解説！②】

前回はなぜルートを使うかというお話までしかできなかったので、今日はルートを使って問題を解く際に気を付けていただきたいことを説明します！！

なぜ±√12は×になるかもしれないの…？

12の平方根を答えなさいという問題、前回のままの考え方で答えると、±√12が答えになりますね！

でも実はこの答えはテストで×になるかもしれないんです…。

√を使っているし、きちんと±も書いているのに、

なぜ×になるのでしょうか…？

それは、√の中の数を簡単な数に書きかえることができるのに、そのままにしているからなんです。

では、±√12は、どのようにして簡単な数に書きかえればよいのでしょうか？

それをこれから説明します！！

数学の基本！答えは簡単な数で書くこと！

テストの問題の答えが分数になった時、約分をしていないと×や△になったことはありませんか？

同じように、√の中の数も簡単な数に書きかえる必要があります。

だから±√12も√の中の数を簡単な数に書きかえないと×や△になるかもしれないのです。

計算したままの数でも〇を付けてもらえることもありますが、先生によっては×や△になることもあるので、答えを書く時は簡単な数に書きかえるようにしましょう！！

√の中で同じ数が2つ揃うと…？

±√12の話をする前に、√の計算について説明します。

この覚え方は教科書通りではないので、こういう考え方もあるんだな、という気持ちで読んでくださいね(^^)/

√の計算の中のルールの1つに√を2乗するとルートが消えるというものがありますが、

√の中の数に同じ数が2つそろったらその数が1つにまとまって√が消える！

と思って計算するのはいかがでしょうか？

ぷよぷよやパ〇ドラみたいな感覚で「√の中の数が同じものが2つそろったら1つにまとまって√が消える」と覚えたら計算が楽しくなりませんか？

例えば、

+√2の2乗なら

+√2²＝2

+√2×(+√2)で√の中の数が同じものがそろったので2が一つにまとまって√が消えます！

(-√5)の2乗なら

(-√5)²＝5

(-√5)×(-√5)で√の中の数が同じものがそろったので5がひとつにまとまって√が消えます！

√の前の+-がそろっていなくても√の中が同じものが2つそろったらルートが消えます！

-√5×(+√5)＝-5

※√の前の符号が(-)×(+)なので(-)となります。

では、確認問題で確認してみましょう！

確認問題

• +√27²＝□
• (-√3)²＝□
• (-√6)×(+√6)＝□

答えは

• 27
• 3
• -6

です！

どうでしょうか？

難しく考えず、ゲーム感覚でルートの中で同じ数が2つ揃っていないか確認しましょう！

√を使った数も簡単にすべし！！

では、±√12を簡単な数に書きかえてみましょう！

簡単な数で書くためには、まずは±√の中の数に注目します！

例として±√12で説明します。

±√12の±√の中の数は12です。

12ってある数をかけ算してできている数ですよね？

±√を簡単な数に書き換える時には、まずは±√の中の数がかけ算してできる数かを確かめます。

±√の中の数が何をかけ算してできた数かは、素因数分解で調べることができます。

では、12を素因数分解してみましょう！

12を素因数分解すると3×2×2ですね！

なので±√12を±√3×2×2と書き換えることができます。

ここで重要なのが、

「√の中の数が同じものが2つそろったら1つにまとまって√が消える」

ということです！

±√3×2×2は、±√の中に2が2つ揃っていますね！

ということで、この2つ揃っている2を一つにまとめて√を消します！

±√を消した数は±と√の間に書きましょう！

こたえ　±2√3

これで完了です。

±√12を簡単な数に書き換える方法、

ちょっとややこしいですが覚えておきましょう！

では、一緒に例題を解いておさらいしてみましょう！

例題：27の平方根を答えなさい。

まずは27を素因数分解してみましょう。

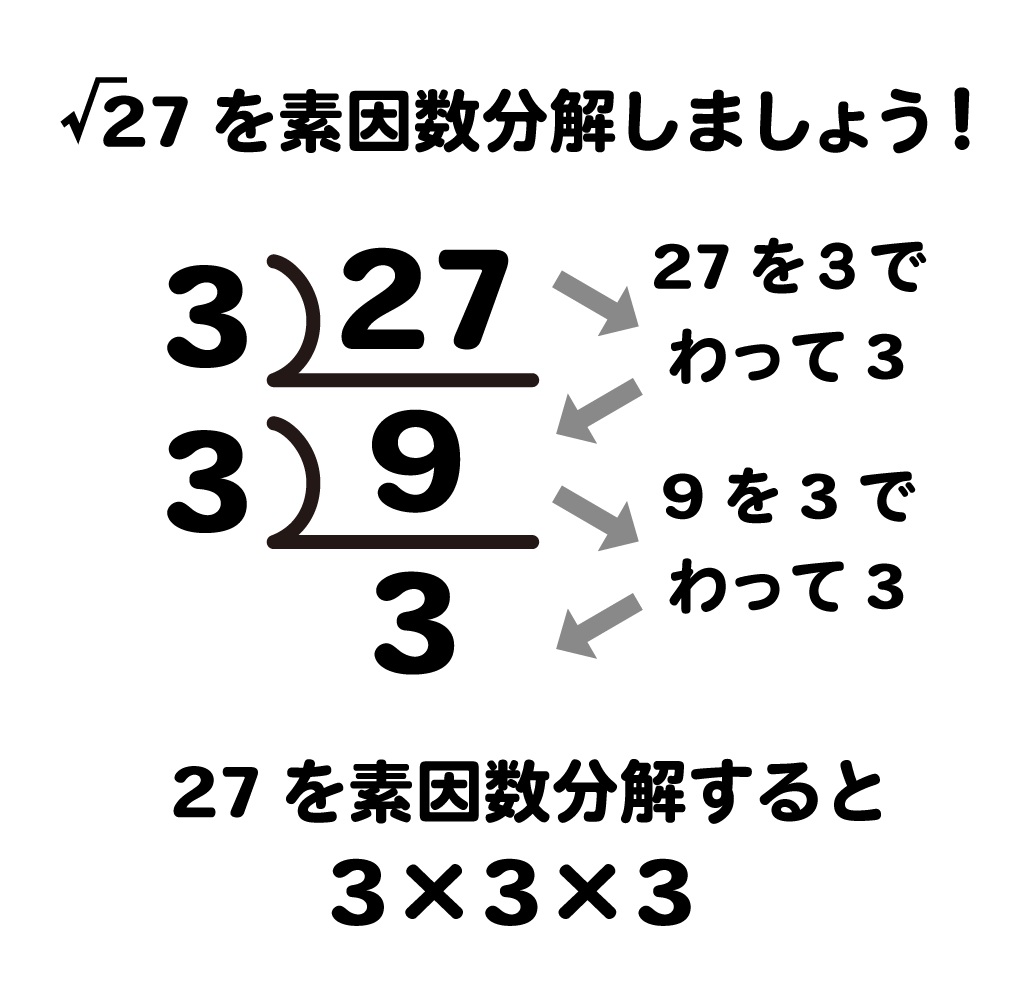
27を素因数分解すると3×3×3となります。

±√27は±√3×3×3と書き換えることができます。

√の中で2つそろっている数はありますか？

今回の±√3×3×3の場合、3が3つあります。

このような場合は、2つそろっている3と1つだけの3という風に数字を見ます。

2つそろっている3の√を消して、1つだけの3に√を付けたままにします。

答えを書く時には√を消した数を±と√の間に書きます。

答え　±3√3

では、次の問題はどうでしょうか？

例題①：50の平方根を答えなさい

50を素因数分解して、

±√の中にいれて、

2つ揃っている数の√を消して、残った数は√の中に入れたままにして…

こたえ　±5√2

次の問題↓

例題②：40の平方根を答えなさい。

40は素因数分解をすると

2×2×2×5になります。

今回は2つそろっている2の√を消して、

2×5は√の中に残します。

こたえ　±2√10

√の中で2つそろっている数の√を消せばOKなので、

「素因数分解をして2つ揃っている数を探す⇒2つそろっている数を一つにまとめてルートを消す」を覚えておきましょう！

この簡単な数に書き換えるのは、どんな問題でも必要です！

教科書通りの覚え方ではありませんが、よかったら覚えておいてください (^^)/

今日の解説は以上です！

教科書通りの解き方ではないですが、少しでもお役に立てれば幸いです(^^)/
　
　
　
　
　
最後までお読みくださりありがとうございます♪
実際に、このブログに登場した先生に勉強の相談をすることも出来ます！
「ブログだけでは物足りない」、「もっと先生に色々教えてほしい！」と感じたあなた、
ぜひ無料体験・相談をして実際に先生に教えてもらいましょう！
友だちも誘って、ぜひ一度体験しに来てくださいね！